QuickDraw 模型训练 & CNN 卷积自学记录

好问题 👍。我帮你把 QuickDraw 数据处理 → CNN 卷积提取特征 → Loss 计算 → Forward & Backward（反向传播） 全流程讲清楚，并配一张图解。

---

1. QuickDraw 数据处理流程

QuickDraw 原始数据是用户手绘的线条（stroke sequence），通常存储为 .npy 或 .npz 格式，里面是 28×28 灰度图。在训练 CNN 前，需要：

1. 读取：加载 .npy 文件，得到 (N, 28, 28) 图像数组。
2. 归一化：像素值从 [0,255] → [0,1]，方便梯度下降。
3. 标签 one-hot：345 类别 → 转成 (345,) 的 one-hot 向量。
4. 划分数据集：train / validation / test。

最终输入网络的就是：
(batch_size, 28, 28, 1) 的张量。

---

2. CNN 卷积层工作原理

CNN 主要做两件事：

• 卷积 (Convolution)：小卷积核（比如 3×3×输入通道）在图像上滑动，提取边缘/形状特征。
• 池化 (Pooling)：缩小空间尺寸（比如 max pooling），保留主要特征。

例子：

• 输入：28×28×1（灰度图）
• 卷积核：3×3×1 → 输出 26×26×32（32 个特征图）
• 再池化：13×13×32
• 重复卷积 → 提取更抽象的形状特征（比如圆、直线）。

---

3. Loss 函数（交叉熵）

QuickDraw 是 多分类问题（345 类）。常用 Loss：

$$L = -\sum_{i=1}^{345} y_i \cdot \log(\hat{y}_i)$$

• ：真实标签（one-hot，只有一个 1）
• ：softmax 输出的概率
  目标：最大化正确类别的概率。

---

4. Forward Propagation（前向传播）

1. 输入图像 → 卷积层（提取边缘特征）
2. → 池化层（降维）
3. → 更深卷积（提取复杂形状）
4. → Flatten → 全连接层
5. → Softmax 输出 345 维概率

---

5. Backward Propagation（反向传播）

训练时，模型计算 Loss，再进行梯度更新：

1. 计算 Loss 对输出的梯度
   
2. 反向传播到全连接层：更新权重 W, b
3. 传播到卷积层：通过卷积核的梯度公式更新 filter 参数
4. 传播到输入层（理论上，但一般不更新输入）

5. 优化器（如 Adam / SGD） 用学习率 η 更新参数：

   $$W = W - \eta \cdot \frac{\partial L}{\partial W}$$

---

6. 图解（流程示意）

QuickDraw 数据 (28x28) ──► [归一化] ──► CNN 卷积提取边缘特征 ──► 池化
                                                     │
                                                     ▼
                                  更深卷积（形状特征，如圆/直线）
                                                     │
                                                     ▼
                                        Flatten → Dense (256)
                                                     │
                                                     ▼
                                        Softmax (345 类)
                                                     │
                                                     ▼
                             交叉熵 Loss (真实标签 vs 预测标签)
                                                     │
                                                     ▼
                                  Backpropagation (梯度反传)
                                                     │
                                                     ▼
                                 更新 CNN 卷积核 & Dense 权重

---

这样一轮就是 一次 forward + backward，不断迭代直到 Loss 收敛。

---

这个问题问得好 ✅，我帮你从 定义 → 为什么要做 → 在 QuickDraw 中的作用 来解释「归一化」。

---

1. 什么是归一化？

在深度学习里，归一化（Normalization） 指的是把数据调整到一个合适的数值范围。

最常见的几种：

• Min-Max 归一化

  $$x' = \frac{x - \min(x)}{\max(x) - \min(x)}$$

  把数值缩放到 [0,1]。

• 标准化 (Z-score Normalization)

  $$x' = \frac{x - \mu}{\sigma}$$

  把数据调整到均值 0，方差 1。

在图像任务里，通常是：

• 灰度像素 [0, 255] → [0, 1]
• 或者 [0, 255] → [-1, 1]

---

2. 为什么要做归一化？

原因主要有 3 个：

(1) 避免数值过大，梯度爆炸 / 梯度消失

如果输入是 0~255，那么卷积时输出值会很大，softmax 里的 exp() 可能会溢出，导致 训练不稳定。
归一化后，数值变小，梯度更平稳。

---

(2) 提高训练速度，加快收敛

深度学习优化依赖梯度下降。
如果数据在同一量级（比如都在 [0,1]），网络更容易找到合适的更新方向，收敛更快。
否则，有些维度梯度很大，有些很小，优化会「抖动」。

---

(3) 提高准确率，避免模型偏向

例如 QuickDraw 的黑白画，有些人画得深（像素值大），有些人画得浅（像素值小）。
如果不归一化，模型会更关注「画深的人」，忽视「画浅的人」，导致泛化差。
归一化后，把不同画法映射到统一范围，模型更公平地学习特征。

---

3. 在 QuickDraw 中的归一化

QuickDraw 输入是 28×28 灰度图，像素范围 0~255。
常见做法：

x = x.astype("float32") / 255.0

这样图像就变成 0~1，利于 CNN 训练。

---

✅ 总结：
归一化就是把输入数据缩放/调整到更合适的数值范围，避免数值问题，提升收敛速度和模型准确率。

---

完全可以用这个公式来做像素归一化，我们仔细分析一下：

---

1. Min-Max 归一化公式回顾

$$x' = \frac{x - \min(x)}{\max(x) - \min(x)}$$

• 是原始数值（例如像素值）
• 是该数据集或该维度的最小值
• 是该数据集或该维度的最大值
• 是归一化后的结果，范围一定在

---

2. QuickDraw 像素的范围

灰度图像每个像素的取值范围是：

$$x \in [0, 255]$$

所以：

$$\min(x) = 0, \quad \max(x) = 255$$

---

3. 套公式

把 和 代入公式：

$$x' = \frac{x - 0}{255 - 0} = \frac{x}{255}$$

✅ 这样就把原本 0~255 的像素值，线性映射到了 [0,1]。

• 原本 0 → 0
• 原本 255 → 1
• 中间值线性缩放，例如 128 → 128/255 ≈ 0.502

---

4. 为什么线性映射有效？

1. 保留相对亮度：像素越亮，归一化后数值越大，卷积依然能感知明暗差异
2. 便于梯度计算：CNN 处理小数值更稳定，避免梯度爆炸
3. 统一尺度：不同手绘图像亮度不同，通过归一化映射到相同尺度，提高模型泛化

---

总结：

Min-Max 归一化公式是 线性映射，可以把任意数值范围 [min, max] 转换到 [0,1]，在 QuickDraw 中就是把灰度像素 [0,255] 缩放到 [0,1]，训练 CNN 更稳定、高效。

---

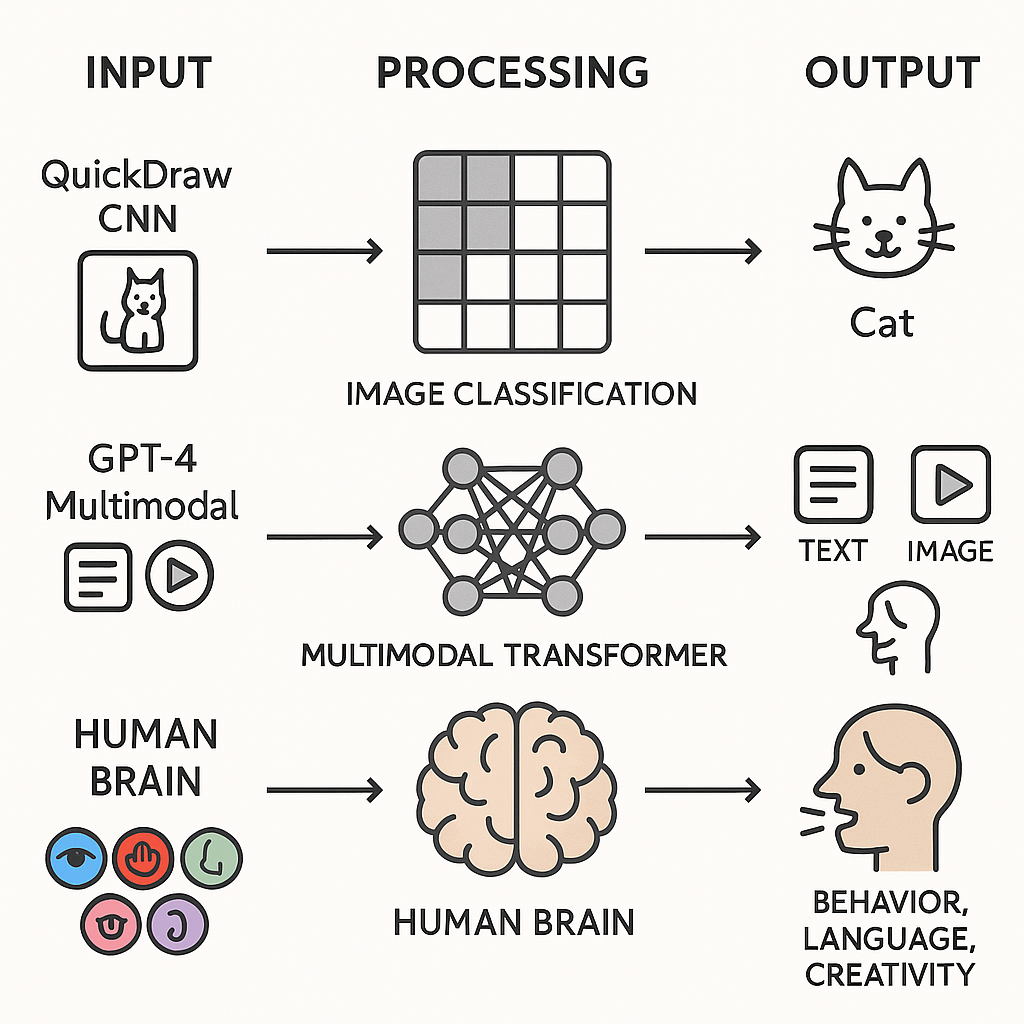
其实我现在很好奇，就是比如我现在训练 quickdraw 的模型，这个就是单一的图像识别模型，而且只能识别出预定好的数据，那如果是像现在 GPT、Gemini 这样的，他们的模型应该除了能分析文字、语法语义、词法以外，还能识别图像，生成图像，生成视频，那他们的模型是单一模型，还是也是多模型，最后根据输入去分门别类找对应模型输出产物？如果模型可以理解是深的大脑，对于人来说，理解外在事物的器官只有一个，如果模型可以理解是深的大脑，对于人来说，理解外在事物的器官只有一个。那目前的 AI 模型是否已经到达人类大脑的运算能力

你问的这个问题其实触及了现代 AI 模型架构、认知类比和算力极限几个层面，我帮你分层解析一下。

---

1️⃣ 单一模型 vs 多模型

QuickDraw 模型

• 你现在训练的 QuickDraw CNN 模型：

  • 输入：28×28 灰度图
  • 输出：345 个类别的概率
  • 单一任务单一模型，只做图像分类
• 这个模型是 窄人工智能（Narrow AI）：只能做训练时定义好的任务，无法做其他类型任务。

GPT/Gemini 类多模态模型

• 现代大模型，比如 GPT-4、Gemini、LLaMA-Adapter：

  • 输入可以是文本，也可以是图像，甚至一些模型在研究阶段支持视频、音频
  • 输出可以是文本生成、图像生成、回答问题、文本总结等

• 架构上：

  • 通常是一个核心模型（一个 Transformer/大语言模型），但：

    • 对不同模态输入有 专门的嵌入层或编码器（image encoder、text tokenizer）
    • 这些编码器把不同模态的数据映射到同一个 通用向量空间

  • 输出阶段：

    • 再用 task-specific head（例如文本生成 head、图像生成 head）生成对应输出
• 本质上是“一体多能”：底层是同一套大脑网络，只是不同类型输入经过不同的前置处理，然后共享底层理解能力。

---

2️⃣ 模型类比人脑

你说得很形象：

如果模型可以理解是深的大脑，对于人来说，理解外在事物的器官只有一个

• 人脑有视觉皮层、听觉皮层、语言中枢等不同的“输入器官”，但底层计算和认知处理共享大脑神经网络

• 类似地，AI 模型：

  • 图像、文本、语音输入各自经过不同的前置编码器（感官）
  • 编码后的向量进入共享 Transformer 或神经网络（认知核心）
  • 输出再分发到不同任务头（动作/表达）

所以现代多模态模型在架构上正在模拟人脑“单大脑多输入感官”的机制。

---

3️⃣ 算力对比人脑

• 人脑大约有 860 亿个神经元、每个神经元平均连接 7000 个突触

• 现代 AI 模型：

  • GPT-4（2023 年估计）参数在 数百亿到万亿级

  • 单纯参数量大，但：

    • 没有人脑的稀疏、高度并行动态调节能力
    • 记忆、即时学习能力远不如人脑（还要训练好几周才学完）
• 结论：算力上接近人脑特定功能，但整体认知能力、常识推理、跨模态灵活性仍远落后于人类大脑。

---

4️⃣ 总结对比

方面	Narrow AI (QuickDraw)	Multi-modal LLM (GPT/Gemini)	人脑
输入	单一图像	文本/图像/视频/音频	视觉/听觉/触觉/味觉/嗅觉
输出	分类	文本/图像/视频生成	行为、语言、思维、创造
模型结构	单 CNN	核心 Transformer + 模态编码器 + 任务头	神经元网络，分区处理 + 整合
学习方式	训练集学习	大规模预训练 + 少量微调	终身学习
算力	小	百亿/万亿参数	约 860 亿神经元，极高并行

✅ 核心思想：现代大模型越来越像“单大脑多感官”，但算力和灵活性还远不及人类。

---

如果你愿意，我可以帮你画一张 QuickDraw CNN vs GPT-4 多模态 vs 人脑类比图，把“输入-处理-输出”的流程直观画出来，非常直观理解。

你想让我画吗？

好的，我们来系统、深入地讲解 卷积神经网络（CNN）中的卷积操作，包括数学公式的推导、原理以及直觉理解。我会从基础到推导，逐步解释。我们尽量做到既数学严谨又易于理解。

---

1️⃣ CNN 卷积操作的直观理解

卷积在 CNN 中的作用本质是 提取局部特征。

假设输入是一个二维图像 （大小 ），卷积核 （大小 ）在图像上滑动，每次计算局部加权和，从而生成输出特征图 。

直观公式：

$$Y(i, j) = \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} K(m, n) \cdot X(i+m, j+n)$$

• 是输出特征图 的索引。
• 是卷积核内部索引。
• 这就是 二维离散卷积（cross-correlation 形式）。

---

2️⃣ 卷积数学公式推导

卷积的连续定义（信号处理中的卷积）为：

$$(f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) g(t - \tau) d\tau$$

• 是输入信号， 是卷积核（滤波器）。
• 离散图像中，积分变成求和：

$$(f * g)[i,j] = \sum_m \sum_n f[m,n] \cdot g[i-m, j-n]$$

在深度学习中，我们通常不做“翻转”，而直接用 cross-correlation：

$$Y[i,j] = \sum_m \sum_n K[m,n] \cdot X[i+m, j+n]$$

⚠ 注意：在数学上严格的卷积会翻转卷积核，但 CNN 框架（TensorFlow、PyTorch）直接用滑动窗口做加权和，更直观。

---

3️⃣ 加入偏置和非线性

CNN 不仅卷积，还会加上偏置 并经过激活函数 ：

$$Y(i,j) = \sigma \Bigg( \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} K(m,n) \cdot X(i+m,j+n) + b \Bigg)$$

• 常用 ReLU、Sigmoid 或 Tanh。
• 允许模型学习偏移，增加表示能力。

---

4️⃣ 多通道卷积（RGB 图像）

对于多通道输入（如 RGB 图像 ），卷积公式扩展为：

$$Y(i,j) = \sum_{c=0}^{C-1} \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} K_c(m,n) \cdot X_c(i+m, j+n) + b$$

• 每个卷积核对应输入的所有通道。
• 可以学习组合不同通道的特征。
• 输出通道数量 决定卷积核数量。

---

5️⃣ 卷积原理的推理与证明

卷积之所以能提取特征，可以从 线性代数和信号处理角度理解：

1. 局部感受野
   卷积核只关注局部像素，捕捉局部模式（如边缘、角点）。

2. 平移不变性
   卷积核在整个图像滑动，相同模式无论出现在图像哪个位置都能被检测到。

3. 线性组合 + 非线性映射

   • 卷积 = 局部加权求和 → 相当于对输入空间做线性投影。
   • 激活函数引入非线性 → 可以表示复杂函数。

4. 卷积的矩阵表示（向量化推理）
   可以把卷积写成矩阵乘法：

   $$\text{vec}(Y) = W \cdot \text{vec}(X)$$
   • 其中 是稀疏矩阵，由卷积核重复填充构成。
   • 这样可以证明卷积是对输入做线性变换，但参数数量远少于全连接层 → 提升计算效率和泛化能力。

---

6️⃣ 卷积公式总结

单通道二维卷积：

$$Y(i,j) = \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} K(m,n) \cdot X(i+m,j+n)$$

多通道卷积：

$$Y(i,j) = \sum_{c=0}^{C-1} \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} K_c(m,n) \cdot X_c(i+m, j+n) + b$$

加非线性激活：

$$Y(i,j) = \sigma \Big( \sum_{c=0}^{C-1} \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} K_c(m,n) \cdot X_c(i+m, j+n) + b \Big)$$

---

7️⃣ 卷积的本质理解

• 特征提取器：卷积核自动学习边缘、纹理、形状等模式。
• 参数共享：同一个卷积核滑动全图 → 节省参数、提高泛化。
• 稀疏连接：每个输出只依赖局部输入 → 控制计算量。

换句话说，CNN 的卷积层通过这种 局部加权求和 + 非线性映射，实现了对图像特征的高效编码。

---

如果你愿意，我可以帮你画一张 卷积数学公式和滑动窗口对应图示，直观展示每个像素和卷积核的关系，并标注公式中的每一项对应图像位置。这样理解卷积公式就更直观了。

你希望我画吗？

卷积、积分、二重/多重级数的关系是什么

好的，我们来系统梳理 卷积、积分、二重/多重级数（求和）的关系，从连续到离散，再到高维，理清它们的数学联系。

---

1️⃣ 卷积与积分的关系（连续情况）

连续信号 和 的卷积定义是：

$$(f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) g(t - \tau) \, d\tau$$

• 积分本质上是连续求和。
• 卷积可以看作对输入信号 进行 滑动加权平均，权重由 决定。
• 积分起到“累加局部贡献”的作用。

🔹 直觉：把卷积理解为“把一个函数翻转、平移，然后做积分求和”，就是连续情况下的“滑动窗口加权求和”。

---

1.1 二维卷积（图像的积分形式）

对于二维连续信号 ：

$$(f * g)(x, y) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\xi, \eta) \, g(x-\xi, y-\eta) \, d\xi \, d\eta$$

• 这是 二重积分，相当于把二维卷积核 在输入图像上滑动，每个位置做加权累积。
• 如果再扩展到三维（例如视频或体数据），就变成 三重积分。

🔹 结论：卷积是积分的一种特殊形式，用于计算一个函数在另一个函数上的加权累积。

---

2️⃣ 离散卷积与级数（求和）的关系

离散信号 的卷积定义：

$$y[n] = (x * h)[n] = \sum_{k=-\infty}^{\infty} x[k] \, h[n - k]$$

• 这里的求和就是 级数（series）。
• 可以看作积分的离散化：积分 → 连续求和，求和 → 离散积分。

2.1 二维离散卷积

对于图像 和卷积核 ：

$$Y[i,j] = \sum_m \sum_n X[i+m, j+n] \, K[m,n]$$

• 二重级数（double sum）：相当于二维积分的离散化。
• 多通道或三维卷积则对应 三重或更高重级数。

---

3️⃣ 总结卷积、积分、级数的关系

类型	表达式	说明
连续一维		积分形式卷积，累加连续贡献
连续二维		二重积分，图像卷积的理论基础
离散一维		积分离散化 → 级数求和
离散二维		二重级数求和，对应图像卷积
离散多维		多重级数，卷积推广到高维

🔹 核心思想：

• 积分 ↔ 连续卷积
• 求和（级数） ↔ 离散卷积
• 单重 ↔ 一维卷积，二重 ↔ 二维卷积，多重 ↔ 高维卷积

---

4️⃣ 小结

1. 卷积就是加权累积，连续情况用积分，离散情况用求和。
2. 二维或高维卷积只是积分/求和维度增加。
3. 离散卷积可以看作连续卷积的采样版。
4. CNN 中卷积本质就是离散多重级数 + 非线性激活的组合。

---

如果你想，我可以画一张 卷积 ↔ 积分 ↔ 二重/多重求和的对照图，直观显示从连续到离散、从一维到二维的对应关系，非常适合理解 CNN 卷积的本质。

你希望我画吗？

$$
(f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) g(t - \tau) \, d\tau

$$ 中输入信号 𝑓(𝜏) 这个函数具体代表什么

好的，我们来仔细分析这个公式中的 究竟代表什么。

---

公式回顾：

$$(f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) \, g(t - \tau) \, d\tau$$

• 和 都是函数， 是积分变量， 是卷积结果的自变量。

---

1️⃣ 的意义

在卷积的语境下，通常我们把 称为 输入信号（input signal）：

• 它是我们希望处理、分析或者提取特征的信号。
• 可以是 时间信号、空间信号、甚至更高维信号。
• 是信号的“自变量”，例如时间、空间坐标等。

例子：

1. 音频信号

   • 是声音的振幅随时间变化的函数。
   • 表示时间（秒或毫秒）。
   • 卷积可以实现滤波器效果，比如低通、高通、回声等。

2. 图像信号（二维）

   • 将二维图像表示为 或在一维展开为 。
   • 可以理解为像素索引或者像素位置。
   • 卷积核 用来提取边缘、纹理、形状等局部特征。

3. 概率密度函数（统计卷积）

   • 也可以是随机变量的概率密度函数。
   • 卷积对应两个随机变量的和的分布。

---

2️⃣ 卷积公式中的角色

$$(f * g)(t) = \int f(\tau) \, g(t-\tau) \, d\tau$$

• → 原始信号，提供“被加权的数值”。
• → 滤波器 / 卷积核，提供“权重”或“响应”。
• 积分 → 对所有位置 的累积，得到在 时刻的输出值。

🔹 直觉：卷积就是“在每个输出时刻 把整个输入信号 和一个翻转平移后的卷积核 做加权累加”。

---

3️⃣ 小结

• 是待处理的输入信号，它决定了卷积输出的基本形状。
• 是积分变量，用于在整个输入信号上“滑动”卷积核。
• 是“响应函数”或卷积核，起到选择性放大或抑制 的作用。
• 卷积的输出 是在每个 时刻对整个信号的加权累积。

---

如果你需要，我可以画一张 、 和卷积输出 的示意图，把公式中每一部分对应的信号形态画出来，这样理解会直观很多。

你希望我画吗？

𝑔(𝑡−𝜏) 滤波器 / 卷积核，又是怎么得来的，不同模型是不一样的吗？不同模型中 𝑓(𝜏) 和 𝑔(𝑡−𝜏) 函数的解析式是不一样的吗？怎么获得对应的解析式

明白，我们来仔细分析卷积公式中 的来源，以及不同模型中 和 的差异与解析式问题。

---

1️⃣ 的本质

公式回顾：

$$(f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) \, g(t-\tau) \, d\tau$$

• → 输入信号（已知数据或者待分析信号）。
• → 卷积核（滤波器），提供 加权响应。

1.1 连续信号中的滤波器

在信号处理领域，卷积核 通常是人为设计的滤波器，例如：

卷积核类型	数学解析式	功能
低通滤波器		平滑信号，去噪
高通滤波器		强调高频边缘
均值滤波器		平滑信号

⚠ 这里的 是已知解析式，人为设计的。

1.2 离散情况（CNN 卷积核）

在 CNN 中：

• → 输入图像或特征图。
• → 卷积核参数，需要 学习得到，通常是随机初始化后通过梯度下降优化得到。
• 没有固定解析式，解析式是模型训练结果：每个卷积核 是一组数值（权重矩阵）。

直觉：

• CNN 卷积核是“自适应滤波器”，自动学习哪些模式重要（边缘、纹理、形状）。
• 不同模型、不同卷积层得到的卷积核是不同的，所以 在不同模型中不一样。
• 训练后，卷积核就是 离散权值矩阵，不一定有简单闭式解析式。

---

2️⃣ 和 的解析式问题

2.1 信号处理（传统滤波）

• → 原始信号，通常有解析式（例如正弦、指数函数）。
• → 滤波器核，有设计公式。
• 卷积结果可以通过积分算出闭式表达（如果解析式简单）。

2.2 神经网络（CNN）

• → 离散输入数据（图像像素），没有简单解析式，只是一组离散数值。
• → 卷积核参数矩阵，通过训练学习得到，也没有固定解析式。
• 输出 → 离散加权和，通常是数值计算得到，不是闭式公式。

⚠ 重点：

• 信号处理卷积 → 解析式可能存在（依赖输入信号和滤波器公式）。
• 深度学习卷积 → 卷积核参数和输入都是离散的数值，解析式通常不存在，只能数值计算。

---

3️⃣ 卷积核是怎么获得的？

3.1 信号处理滤波器（人工设计）

• 根据需求选择低通、高通、带通等滤波器。
• 公式直接写出来，例如高斯核、Sobel 算子等。

3.2 CNN 卷积核（训练学习）

训练过程：

1. 初始化卷积核 （通常随机或 Xavier/He 初始化）。
2. 输入 经过卷积 + 激活 → 输出预测。
3. 与真实标签计算损失函数 。
4. 反向传播梯度 更新卷积核权重。
5. 训练多轮迭代后，卷积核 收敛 → 自动学会特征提取。

🔹 所以 CNN 中卷积核 不是人工公式，而是学习得到的数值矩阵。

---

4️⃣ 总结

项目	信号处理卷积	CNN 卷积
	连续或离散信号，可能有解析式	离散数据（图像/特征），通常无解析式
	人工设计滤波器，解析式已知	卷积核参数矩阵，训练学习得到，无解析式
获得方式	根据设计公式	通过梯度下降训练得到
输出	积分或求和，可求解析式	离散卷积，数值计算得到

---

如果你愿意，我可以画一张 卷积核从设计到学习的对比图，清晰展示 在信号处理和 CNN 中的差异，以及训练是如何得到卷积核的。

你希望我画吗？

“𝑔 → 卷积核参数，需要 学习得到，通常是随机初始化后通过梯度下降优化得到” 这个是通过实验图像设计的吗，还是怎么设计的，具体怎么得到呢

明白，我来详细讲清楚 CNN 中卷积核 具体是怎么得到的，以及为什么说是“学习得到”，而不是人工设计。我们分步骤仔细分析。

---

1️⃣ 卷积核不是手工设计的

在 CNN 里，卷积核 并不是你根据图像人工设计的（不像传统滤波器，例如 Sobel 边缘算子或高斯平滑）。

原因：

• 手工设计需要先知道要提取的特征类型（边缘、纹理、角点），这是先验知识。
• CNN 的优势是自动发现有用特征，无需人工指定。
• 不同任务、不同数据集的卷积核可能完全不同。

换句话说，卷积核是数据驱动的，由训练过程自动优化。

---

2️⃣ 卷积核的初始化

训练前，卷积核 需要初始化：

• 随机初始化：常用高斯或均匀分布生成初始权重。
• Xavier/He 初始化：根据前后层神经元数量调整初始值，避免梯度消失或爆炸。

这个阶段，卷积核只是随机数矩阵，并没有特定含义。

例如一个 3×3 卷积核初始化：

$$g = \begin{bmatrix} 0.02 & -0.01 & 0.05 \\ -0.03 & 0.10 & 0.01 \\ 0.04 & -0.02 & 0.03 \end{bmatrix}$$

---

3️⃣ 卷积核的学习过程

卷积核真正有意义，是在 训练过程中通过梯度下降学习得到：

3.1 前向传播

1. 输入图像 与卷积核 卷积 → 输出特征图 。
2. 特征图经过激活函数、池化等处理 → 最终得到预测值 。

3.2 计算损失

• 预测值 与真实标签 计算损失函数 。
• 例如分类任务用交叉熵损失，回归任务用均方误差。

3.3 反向传播（Backpropagation）

• 对卷积核 计算梯度：

$$\frac{\partial L}{\partial g} = \text{链式法则传播损失到卷积核}$$

• 梯度表示卷积核中每个元素应该如何调整才能让预测更准确。

3.4 参数更新（梯度下降/Adam）

• 更新卷积核：

$$g \gets g - \eta \frac{\partial L}{\partial g}$$

• 是学习率。
• 多轮迭代后，卷积核自动学会提取“对任务最有用的特征”。

---

4️⃣ 举例直观理解

假设你训练 CNN 做猫狗分类：

• 第一层卷积核可能学会检测边缘、方向线条，类似 Sobel 滤波器。
• 第二层卷积核可能学会检测局部纹理、耳朵或毛发模式。
• 第三层卷积核可能学会组合前面特征，识别猫耳朵+眼睛+鼻子模式。

这里的卷积核不是实验设计的，而是通过大量图像训练得到的数值矩阵。

---

5️⃣ 总结

1. 卷积核 初始阶段是随机数（或特殊初始化）。
2. 训练过程中通过梯度下降优化，逐渐变成能提取任务相关特征的权重矩阵。
3. CNN 卷积核不需要人工设计，完全依赖数据和损失函数来学习。
4. 训练结束后，卷积核就是模型的“特征提取器”，数值上可以看作滤波器，但没有固定解析公式。

---

如果你想，我可以画一张 卷积核从随机初始化 → 梯度更新 → 学会边缘/纹理特征 的图，直观展示 CNN 是怎么“自己设计卷积核”的。

你希望我画吗？